Talk is cheap，上代码。基于标准C++实现。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include <random>
#include <iostream>
#include <ctime>
#include <algorithm>
#define KB(x) ((size_t)(x) << 10)
using namespace std;
int main()
{
    //需要测试的数组大小
    vector<size_t> sizes_KB;
    for (int i = 1; i < 18; i++)
    {
        sizes_KB.push_back(1 << i);
    }
    random_device rd; //随机数生成
    mt19937 gen(rd());
    for (size_t size : sizes_KB)
    {
        uniform_int_distribution<> dis(0, KB(size) - 1);
        vector<char> memory(KB(size)); //创建一个指定大小的连续内存块
        fill(memory.begin(), memory.end(), 1);
        int dummy = 0; //用这个变量避免编译器对下面的循环进行优化
        //在内存块上进行大量的随机访问，并计时
        clock_t begin = clock();
        for (int i = 0; i < (1 << 25); i++)
        {
            dummy += memory[dis(gen)];
        }
        clock_t end = clock();
        double elapsed_secs = double(end - begin) / CLOCKS_PER_SEC;
        cout << size << " KB, " << elapsed_secs << "secs, dummy:" << dummy << endl;
    }
    cin.get();
}

思路很简单：
创建一个连续内存块，进行连贯、大量、随机的有意义内存访问。这几点缺一不可，否则不能保证整块内存被尽可能的放入Cache。在这种情况下，当内存块能够被整块放入Cache时，平均访问速度会显著的快。观察随着内存大小提高，平均访问时间的跃升点，即可估计Cache大小。代码说明：vector内部是连续内存块。通过累加并输出一个dummy变量，使得内存访问变得有意义，否则很可能被优化掉。
输出结果如下：
img
将结果绘图：
img

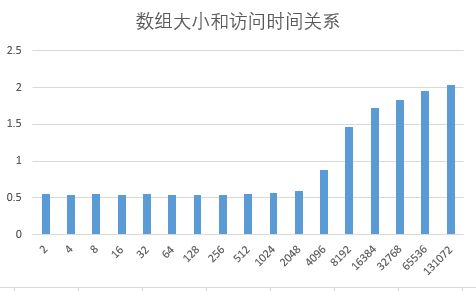
可见4096K以下时，访问时间基本固定，但是4096K之后访问时间有一个跃升。可见某一级的Cache大小约为4096K （4M）.测试用的CPU是i7-6500U，信息如下：
img

与测试结果接近。

这个方法正如上面 @陈昱所说，CSAPP封面那个图就是这样搞的。
img
我有一本CSAPP的作者签名版，液~！